
当前课程知识点:概率论 > 第一章 随机事件及其概率 > 第四节 条件概率 > 知识拓展:三门概率问题
聪明人的三门问题
三门问题又被称为蒙提霍尔问题,出自美国一个电视益智游戏节目,这个问题一被提出就引起了相当大的争议。
在一次有奖竞猜活动中,参赛者需要面对三扇门的诱惑。参赛者会看见三扇关着的门,其中一扇门的后面藏有一辆汽车,选中这扇门就可以获得汽车,而另外两扇门后面则各藏有一头山羊。虽然山羊和汽车一样都可以充当交通工具,但和汽车相比起来,山羊还是便宜了一些,所以参赛者的目标是——选中汽车。
当参赛者选定了一扇门但还未打开它的时候,知道门后情况的节目主持人打开另外两扇门中的一扇,出现了一头山羊。然后,主持人会问参赛者要不要改变主意选择另一扇关着的门。这时,参赛者就有这样的疑问了:换另一扇门是否会增加获得汽车的概率?
假设参赛者最初选择的是1号门,现在主持人打开了3号门,后面是一头山羊。如果你是参赛者,你会改变主意选择2号门吗?
对于这个问题,一位高智商女性玛丽莲·莎凡特给出了她的答案,她认为参赛者应该改变主意选择2号门,因为这个选择将会使他获得汽车的概率增加一倍。这个答案引起了轩然大波,因为它不合乎大多数人的直觉。
事实上,大多数人的回答都是“不改变主意,坚持选择1号门”。他们认为不应该更换选择,因为汽车在哪扇门的后面是不能改变的,无论改不改变选择,参赛者选中汽车的概率都是50%。所以,顺从自己最初的直觉会比较好。
玛丽莲给出自己的答案后,数千封投诉信纷至沓来。但很快,她漂亮地解释了自己的答案,让大家心服口服。她是怎么解释的呢?
参赛者选中一扇门时,有三种可能情况,它们的概率相等,都是1/3:
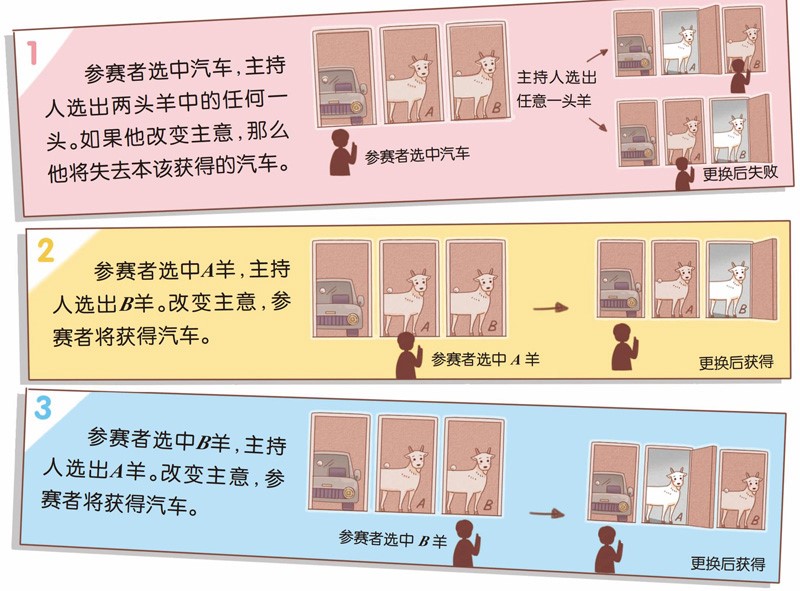
我们对比一下会发现,在后两种情况下,参赛者都可以通过更换选择而获得汽车。第一种情况是唯一一种参赛者更换选择会吃亏的情况,所以改变主意而获得汽车的概率是2/3。
我们还可以用逆向思维来理解:
无论参赛者开始的选择是什么,在被主持人问到是否更换时都选择更换。如果参赛者先选中山羊,那么更换后会获得汽车;如果参赛者先选中汽车,那么更换后会失去汽车。而选中山羊的概率是2/3,选中汽车的概率是1/3。所以选择更换是明智的,相对最初获得汽车仅为1/3的概率来说,改变选择可以增加获得汽车的可能性。
三门问题是一个老问题了,不过它在任何时候都能引起激烈的争论。总结一下,正确答案应该是:如果主持人事先知道哪扇门后面有山羊,并且她特意选择把有山羊的那扇门打开,那么参赛者应该更换选择另一扇门,这可以使获得汽车的概率从1/3 升到2/3。
换还是不换?大部分人之所以会左右为难,是因为他们常常把自己最初就选中汽车的概率想得太高。如果我们将三门问题升级一下,或许就好理解了。
现在,我们试试另一个挑战,我们将它称作“百门问题”。一百扇门中只有一扇后面藏有汽车,其余藏的都是山羊。请你先随心所欲选中一扇门。

选好了吗?假设你选了1号门。不过,你应该对这个选择不抱什么希望——能一次就选中汽车的概率太低了,只有1%的可能。这时,主持人将剩下99扇门中的98扇打开,它们的后面全是山羊。也就是说,汽车在没有被打开的1号门或37号门后面。
-第一节 基本概念
--1.1.2 三个基本概念(随机试验、样本空间、随机事件)
--三个基本概念课件
--事件的关系课件
--第一章第一节作业
-第二节 事件的概率
--概率的定义课件
--概率的性质课件
--概率的定义课件
--概率的性质课件
--第一章第二节作业
-第三节 古典概率
--古典概率课件
--知识拓展:几何概型之蒲丰投针问题(圆周率估算的一种方式)
--几何概型课件
--第一章第三节作业
-第四节 条件概率
--乘法公式课件
--贝叶斯公式课件
--全概率公式课件
--第一章第四节作业
-第五节 事件的独立性
--事件的独立性课件
--第一章第五节作业
-第一节 随机变量的定义
--第二章第一节作业
-第二节 分布函数的定义
--第二章第二节作业
-第三节 离散型随机变量
--第二章第三节作业
--泊松分布课件
-第四节 连续型随机变量
--均匀分布课件
--指数分布课件
--第二章第四节作业
-第五节 一维随机变量函数的分布
--第二章第五节作业
-第一节 多维随机变量的联合分布
--第三章第一节作业
-第二节 二维离散型随机变量
--第三章第二节作业
-第三节 二维连续型随机变量
--第三章第三节作业
-第四节 边缘分布
--第三章第四节作业
-第五节 随机变量的独立性
--第三章第五次作业
-第一节 随机变量的数学期望
--第四章第一节作业
-第二节 随机变量的方差
--第四章第二节作业
--方差的性质课件
-第一节 大数定律
--第五章第一节作业
--大数定律课件
-第二节 中心极限定理
--第五章第二节作业




